1. Introduction

2. La base 2 (binaire) , la base 10 (décimal)

• La base 10
• La base 2
• Conversion binaire vers décimale.
• Conversion décimale vers binaire
• Python est le binaire

3. Codage des caractères

• ASCII
• ISO-8859-1 (Latin-1)
• Unicode (UTF-8)

4. La base 16 (héxadécimale)

• Conversion hexadécimale vers décimale
• Conversion hexadécimale vers décimale
• Python est le changement de base

5. Codage des couleurs

Introduction

La base 2 (binaire) , la base 10 (décimal

LA BASE 10 : Numérotation décimale

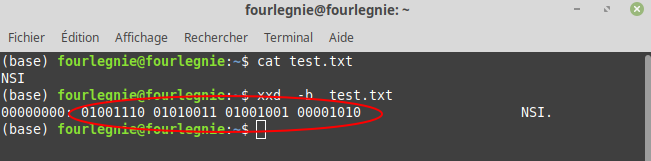
Nous représentons les valeurs entières dans le système décimal, on dit aussi en base 10. Nous utilisons les dix chiffres de 0 à 9. Par exemple, 542 est compris comme

LA BASE 2 : Numérotation binaire

- Capacite d'un nombre (Lien)

L'information numérique, qu'il s'agisse de valeurs entière nombres, de textes, d'images, ou de sons est représentée par des suites de 0 et de 1. On parle de bit : un bit (BInary digiT : chiffre binaire) ) peut prendre deux valeurs, 0 ou 1.

- Méthode : Conversion binaire vers décimale.

Méthode : Conversion décimale vers binaire

C'est assez long puisqu'il faut faire des divisions successives par 2

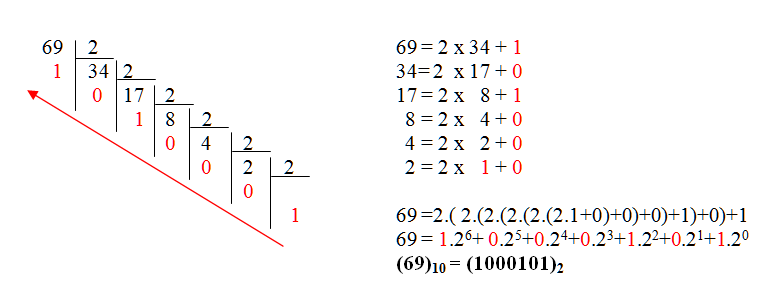
Mais une méthode plus simple consiste à écrire les puissances de 2 successives jusqu'à dépasser la valeur à convertir.

Commencer alors par le bit de poids le plus fort (à gauche). Peut-on le soustraire ? Si oui, activer le bit et continuez de la même manière avec le reste.

Les bits cochés correspondent à des 1, les non cochés à des zéros

Le tableau ci-dessous permet de faire la conversion décimal vers binaire d'un octet.

Source : https://curie-vire.pagesperso-orange.fr

Codage des caractères

ASCII

Avant 1960 de nombreux systèmes de codage de caractères existaient, ils étaient souvent incompatibles entre eux. En 1960, l'organisation internationale de normalisation (ISO) décide de mettre un peu d'ordre dans ce bazar en créant la norme ASCII (American Standard Code for Information Interchange). À chaque caractère est associé un nombre binaire sur 8 bits (1 octet). En faite, seuls 7 bits sont utilisés pour coder un caractère, le 8e bit n'est pas utilisé pour le codage des caractères. Avec 7 bits il est possible de coder jusqu'à 128 caractères ce qui est largement suffisant pour un texte écrit en langue anglaise (pas d'accents et autres lettres particulières).

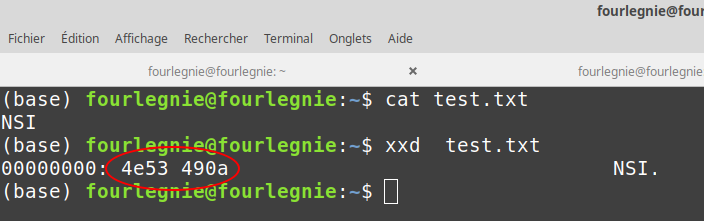
Comme vous pouvez le constater dans le tableau ci-dessus, au "A" majuscule correspond le code binaire (1000001)₂ ((65)₁₀ ou (41)₁₆)

ISO-8859-1

La norme ASCII convient bien à la langue anglaise, mais pose des problèmes dans d'autres langues, par exemple le français. En effet l'ASCII ne prévoit pas d'encoder les lettres accentuées. C'est pour répondre à ce problème qu'est née la norme ISO-8859-1. Cette norme reprend les mêmes principes que l'ASCII, mais les nombres binaires associés à chaque caractère sont codés sur 8 bits, ce qui permet d'encoder jusqu'à 256 caractères. Cette norme va être principalement utilisée dans les pays européens puisqu'elle permet d'encoder les caractères utilisés dans les principales langues européennes (la norme ISO-8859-1 est aussi appelée "latin1" car elle permet d'encoder les caractères de l'alphabet dit "latin")

Problème, il existe beaucoup d'autres langues dans le monde qui n'utilisent pas l'alphabet dit "latin", par exemple le chinois ou le japonnais ! D'autres normes ont donc dû voir le jour, par exemple la norme "GB2312" pour le chinois simplifié ou encore la norme "JIS_X_0208" pour le japonais.

Cette multiplication des normes a très rapidement posé problème. Imaginons un français qui parle le japonais. Son traitement de texte est configuré pour reconnaitre les caractères de l'alphabet "latin" (norme ISO-8859-1). Un ami japonais lui envoie un fichier texte écrit en japonais. Le français devra modifier la configuration de son traitement afin que ce dernier puisse afficher correctement l'alphabet japonais. S'il n'effectue pas ce changement de configuration, il verra s'afficher des caractères ésotériques.

Unicode

Pour éviter ce genre de problème, en 1991 une nouvelle norme a vu le jour : Unicode

Unicode a pour ambition de rassembler tous les caractères existant afin qu'une personne utilisant Unicode puisse, sans changer la configuration de son traitement de texte, à la fois lire des textes en français ou en japonais

Unicode est uniquement une table qui regroupe tous les caractères existant au monde, il ne s'occupe pas de la façon dont les caractères sont codés dans la machine. Unicode accepte plusieurs systèmes de codage : UTF-8, UTF-16, UTF-32. Le plus utilisé, notamment sur le Web, est UTF-8.

Pour encoder les caractères Unicode, UTF-8 utilise un nombre variable d'octets : les caractères "classiques" (les plus couramment utilisés) sont codés sur un octet, alors que des caractères "moins classiques" sont codés sur un nombre d'octets plus important (jusqu'à 4 octets). Un des avantages d'UTF-8 c'est qu'il est totalement compatible avec la norme ASCII : Les caractères Unicode codés avec UTF-8 ont exactement le même code que les mêmes caractères en ASCII.

Avec Python

for i in range(64,127):
    print(chr(i))

for i in range(15000,16000):
    print(chr(i))

Base 16 (Héxadécimale)

Méthode : Conversion hexadécimale vers décimale

Exemple : (3F7A)₁₆=3 x 16³ + 15 x 16² + 7 x 16¹ + 10 x 16⁰ = 15 x 256 + 7 x 16 + 10 x 1 = 16250

Méthode : Conversion hexadécimale vers décimale

45₁₆=4 x 16¹+5=69

A4₁₆=10 x 16¹+4=164

Codage des couleurs

Le Codage R G B des couleurs

<body style="background-color:black;">

<p style="color:red;">
Un paragraphe en rouge</p>

<p style="color:rgb(255,0,255);">
Un paragraphe en violet</p>

<p style="color:#0000FF;">
Un paragraphe en bleu</p>



</body>

Cliquer ici pour voir le rendu du fichier html ci-dessus.

1. par son nom (color:yellow; color:red; color:black; etc),
2. par sa notation décimale (rgb(255,255,0)).
3. par son triplet RGB en utilisant la notation hexadécimale (#FFFF00)

1 octet = 8 bits