Tester search1(10000) et search1(100000000) puis expliquer ce que fait cette fonction.

import random
def search1(taille):
	L=range(taille) 
	nb=random.randint(L[0],L[taille-1])
	for elt in L:
		if elt == nb :
			return "Trouvé"

Compléter la fonction ci-dessous. Cette fonction prend en paramétre un nb taille (taille d'une liste) et renvoie le temps mis pour exécuter 100 fois la fonction search1(taille)

import time
def repeat_search1(taille):
		time1=time.time()
		
		
		
		
		return  temps

Compléter la fonction liste_time_search1(taille_max) qui prend en paramétre un nombre taille_max et qui renvoie une liste telle que :

• Le 1er élément est le temps mis pour executer repeat_search1(1).
• Le 2ème élément est le temps mis pour executer repeat_search1(2).
• Le 3ème élément est le temps mis pour executer repeat_search1(3).
• ...
• Le taille_max ème élément est le temps mis pour executer repeat_search1( taille_max) .

Autrement dit on veut (avec taille_max=1000) :

	L=[]
	L.append(repeat_search1(1))
	L.append(repeat_search1(2))
	L.append(repeat_search1(3))
	...
	L.append(repeat_search1(1000))

def liste_time_search1(taille_max):
	L=[]


	return L

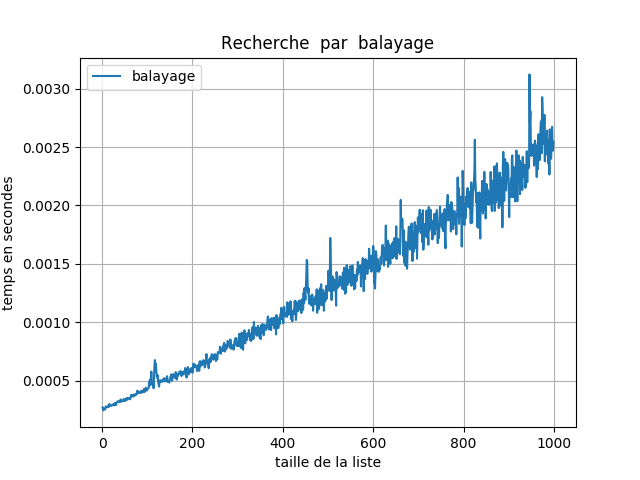
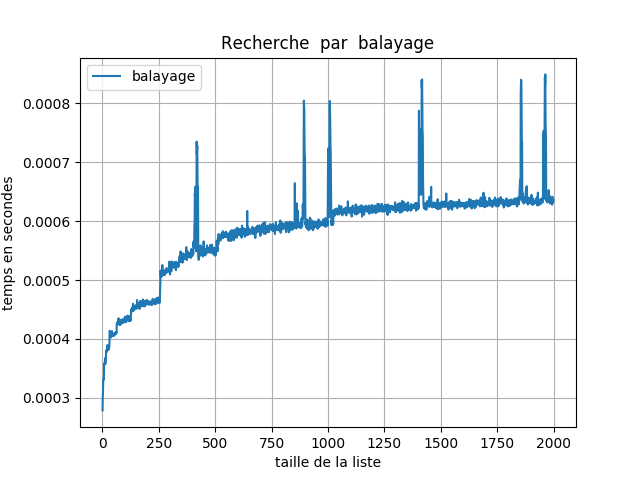
Executer le code ci-dessous avec taille_max = 1000 et 2000 puis en déduire la compléxité de cet algorithme de recherche.

import pylab
def complexite1(taille_max):
    abscisses = [i for i in range(1,taille_max)] 
    ordonnees=liste_time_search1(taille_max)
    pylab.title('Recherche  par  balayage')
    pylab.xlabel('taille de la liste')
    pylab.ylabel('temps en secondes')
    pylab.grid()
    pylab.plot(abscisses,ordonnees,label="balayage")
    pylab.legend()
    pylab.show()

Expliquer la présence des nombreux pics.

Apporter les modifications necessaires pour traiter le balayage dans le pire des cas.

def search2(taille):
    L=range(taille)
    nb=random.randint(L[0],L[taille-1])
    gauche=0
    droite=taille-1
    while gauche < droite:
        milieu=(gauche+droite)//2
        if L[milieu] < nb:
            gauche=milieu+1
        else :
            droite=milieu
    return L[gauche]

Construire le graphique illustrant la compléxite en temps de l'algorithme de recherche par dichotomie.

Aide : Reprendre la démarche du paragraphe ci-dessus.

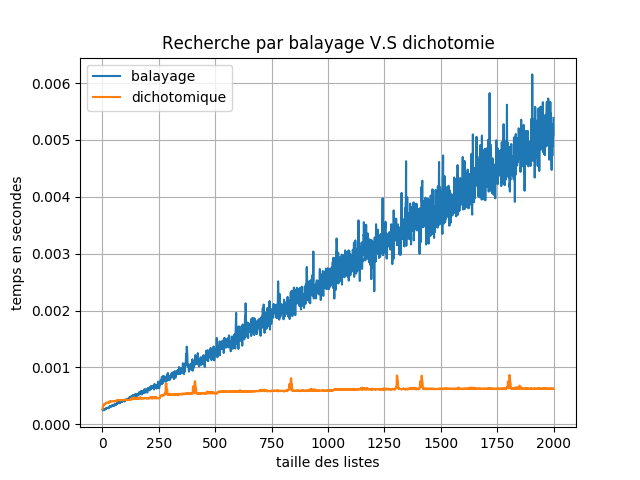
Completer le code ci-dessous de façon à pourvoir comparer (sous la forme d'un graphique) la complexité en temps des deux algorithmes de recherche.

def comparer_complexite(taille_max):
    ordonnees_liste1=        # Mettre la liste optenu avec la méthode "Recherche séquentielle"
    ordonnees_liste2=        # Mettre la liste optenu avec la méthode "Recherche dichotomique"
    abscisses = [i for i in range(1,taille_max)] 
    pylab.title('Recherche par balayage V.S dichotomie')
    pylab.xlabel('taille des listes')
    pylab.ylabel('temps en secondes')
    pylab.grid()
    pylab.plot(abscisses,ordonnees_liste1,label="balayage ")
    pylab.plot(abscisses,ordonnees_liste1,label="dichotomique")
    pylab.legend()
    pylab.show()

1. On effectue une recherche d'un élément par dichotomie dans une liste triée de taille 1000000. Combien de comparaisons sont nécessaires ?
2. Même question avec une taille de 2000000
3. Même question avec une taille de 10000000
4. Defis : Même question avec une taille de n (n est une entier naturel)

Vrai ou faux ? Par rapport à la recherche séquentielle dans une liste, la recherche dichotomique dans une liste triée :

1. est systématiquement plus rapide
2. en moyenne beaucoup plus rapide
3. ne donne pas toujours le bon resultat

1. Ecrire une fonction qui prend en parametre une liste d'entiers et renvoie le second plus petit élément de la liste. S'il n'y en a pas, la fonction devra renvoyer la valeur None

   Par exemple :

   • La liste [4,7,1,-1,3] devra renvoyer 1.
   • La liste [4,7,0,0,3] devra renvoyer 3.
   • La liste [ ] ou [3] ou [5,5] devra renvoyer None .
2. A l'aide d'un graphique, étudier sa complexite en temps
3. Comparer la complexité de votre algorithme avec celle de l'algorithme ci-dessous :

def mon_algo(L):
    if len(L)==0 or len(L)==1:
        return None
    L.sort()
    min=L[0]
    for elt in L:
        if elt != min:
            return elt
    return None