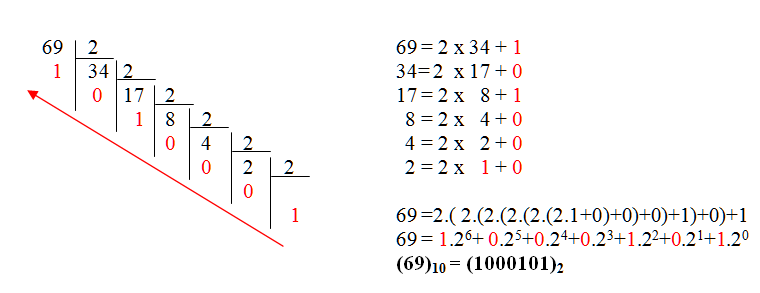Chapitre 2 : Représentation d'un texte en machine


  1. Introduction

  2. La base 2 (binaire) , la base 10 (décimal)

  3. Codage des caractères

  4. La base 16 (héxadécimale)

  5. Python et les chaînes de caractères

Introduction

Voici un fichier texte vu par l'utilisateur :

TP2_NSI_1.png

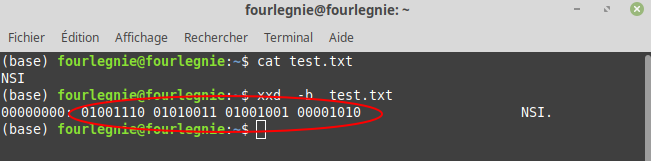
A l'aide d'un terminal, on peut savoir comment le fichier est "perçu" par la machine :

TP2_NSI_2.png

TP2_NSI_2.png


La base 2 (binaire) , la base 10 (décimal

Pourquoi les ordinateurs travaillent avec des 0 et des 1 ?
011101011010011101010011100011000111101111111000001010101111010001110111001110101101001110101001110001100011110111111100000101010111101000111011100111010110100111010100111000110001111011111110000010101011110100011101110

LA BASE 10 : Numérotation décimale

Nous représentons les valeurs entières dans le système décimal, on dit aussi en base 10. Nous utilisons les dix chiffres de 0 à 9. Par exemple, 542 est compris comme

542 = 5 x 100 + 4 x 10 + 2

LA BASE 2 : Numérotation binaire

L'information numérique, qu'il s'agisse de valeurs entière nombres, de textes, d'images, ou de sons est représentée par des suites de 0 et de 1. On parle de bit : un bit (BInary digiT : chiffre binaire) ) peut prendre deux valeurs, 0 ou 1.

1 byte = 1 octet = 8 bits

- Méthode : Conversion binaire vers décimale.


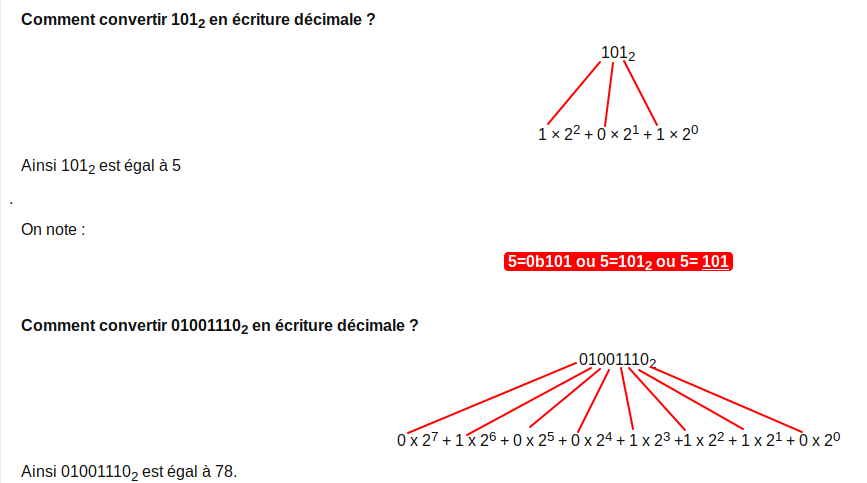
Donnez les valeurs entières représentées par 0b0100, 0b10101, 0b101 et 0b11111.

Quel est le plus grand entier que l'on puisse obtenir avec un octet ?

Quel est le plus grand entier que l'on puisse obtenir avec deux octets ?

Quelle est la représentation binaire de 14 et 78 ?

Méthode : Conversion décimale vers binaire

C'est assez long puisqu'il faut faire des divisions successives par 2

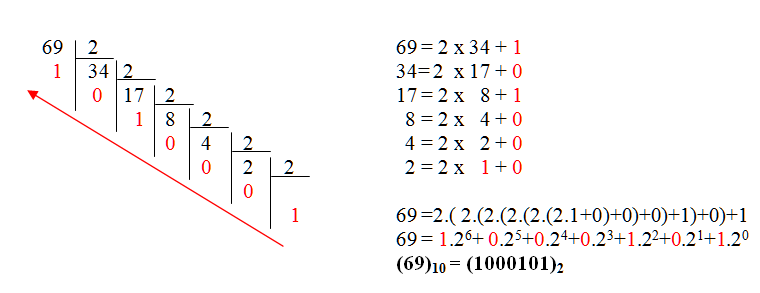
décimal vers binaire

Mais une méthode plus simple consiste à écrire les puissances de 2 successives jusqu'à dépasser la valeur à convertir.

Commencer alors par le bit de poids le plus fort (à gauche). Peut-on le soustraire ? Si oui, activer le bit et continuez de la même manière avec le reste.

Les bits cochés correspondent à des 1, les non cochés à des zéros

Le tableau ci-dessous permet de faire la conversion décimal vers binaire d'un octet.

2726252423222120 Valeur décimale
1286432168421
0 1 1 0 1 1 0 0 108
Source : https://curie-vire.pagesperso-orange.fr

Quelle est la représentation binaire de 123 ?

Quelle est la représentation binaire de 65 ?



Quelle est la représentation binaire de 2048 ?

Quelle est la représentation binaire de 2019 ?

Avec Python

Le langage Python comporte des instructions permettant de passer de la notation binaire à la notation décimale, et inversement.
Par exemple, l’instruction bin(89) renvoie la chaîne de caractères 0b1011001. Le 0bau début indique que la chaîne représente un nombre en binaire ; les 0 et 1 qui suivent sont la représentation en numération binaire.
Inversement, on peut obtenir la valeur décimale d’un nombre en binaire, en écrivant simplement 0b puis la suite de 0 et de 1 qui forment le nombre.
Par exemple, après la commande a=0b10101 , la variable a contient la valeur 21 (numération décimale).

QUIZZ - TESTEZ VOTRE MAITRISE DU BINAIRE

QUIZZ NON FAIT !



Codage des caractères

Nous savons qu'un ordinateur est uniquement capable de traiter des données binaires, comment sont donc codés les textes dans un ordinateur ? Ou plus précisément, comment sont codés les caractères dans un ordinateur ?

ASCII

Avant 1960 de nombreux systèmes de codage de caractères existaient, ils étaient souvent incompatibles entre eux. En 1960, l'organisation internationale de normalisation (ISO) décide de mettre un peu d'ordre dans ce bazar en créant la norme ASCII (American Standard Code for Information Interchange). À chaque caractère est associé un nombre binaire sur 8 bits (1 octet). En faite, seuls 7 bits sont utilisés pour coder un caractère, le 8e bit n'est pas utilisé pour le codage des caractères. Avec 7 bits il est possible de coder jusqu'à 128 caractères ce qui est largement suffisant pour un texte écrit en langue anglaise (pas d'accents et autres lettres particulières).

Comme vous pouvez le constater dans le tableau ci-dessus, au "A" majuscule correspond le code binaire (1000001)2 ((65)10 ou (41)16)

Quel est le code binaire du "a" minuscule en ASCII?

Quelques soucis avec l'encodage Ascii :

Test 1 (ASCII)

Test 2 (ISO-8859-1 ou Latin1)

Test 3 (UTF-8 ou Unicode)


Repérer les différence entre les codes sources.

ISO-8859-1

La norme ASCII convient bien à la langue anglaise, mais pose des problèmes dans d'autres langues, par exemple le français. En effet l'ASCII ne prévoit pas d'encoder les lettres accentuées. C'est pour répondre à ce problème qu'est née la norme ISO-8859-1. Cette norme reprend les mêmes principes que l'ASCII, mais les nombres binaires associés à chaque caractère sont codés sur 8 bits, ce qui permet d'encoder jusqu'à 256 caractères. Cette norme va être principalement utilisée dans les pays européens puisqu'elle permet d'encoder les caractères utilisés dans les principales langues européennes (la norme ISO-8859-1 est aussi appelée "latin1" car elle permet d'encoder les caractères de l'alphabet dit "latin")

Problème, il existe beaucoup d'autres langues dans le monde qui n'utilisent pas l'alphabet dit "latin", par exemple le chinois ou le japonnais ! D'autres normes ont donc dû voir le jour, par exemple la norme "GB2312" pour le chinois simplifié ou encore la norme "JIS_X_0208" pour le japonais.

Cette multiplication des normes a très rapidement posé problème. Imaginons un français qui parle le japonais. Son traitement de texte est configuré pour reconnaitre les caractères de l'alphabet "latin" (norme ISO-8859-1). Un ami japonais lui envoie un fichier texte écrit en japonais. Le français devra modifier la configuration de son traitement afin que ce dernier puisse afficher correctement l'alphabet japonais. S'il n'effectue pas ce changement de configuration, il verra s'afficher des caractères ésotériques.

Unicode

Pour éviter ce genre de problème, en 1991 une nouvelle norme a vu le jour : Unicode

Unicode a pour ambition de rassembler tous les caractères existant afin qu'une personne utilisant Unicode puisse, sans changer la configuration de son traitement de texte, à la fois lire des textes en français ou en japonais

Unicode est uniquement une table qui regroupe tous les caractères existant au monde, il ne s'occupe pas de la façon dont les caractères sont codés dans la machine. Unicode accepte plusieurs systèmes de codage : UTF-8, UTF-16, UTF-32. Le plus utilisé, notamment sur le Web, est UTF-8.

Pour encoder les caractères Unicode, UTF-8 utilise un nombre variable d'octets : les caractères "classiques" (les plus couramment utilisés) sont codés sur un octet, alors que des caractères "moins classiques" sont codés sur un nombre d'octets plus important (jusqu'à 4 octets). Un des avantages d'UTF-8 c'est qu'il est totalement compatible avec la norme ASCII : Les caractères Unicode codés avec UTF-8 ont exactement le même code que les mêmes caractères en ASCII.

Quel est le code binaire du "b" codé avec UTF-8 ?

A l'aide de la table ASCII,

  1. Donnez la représentation binaire du texte suivant :

    ABC

  2. Décoder ce texte.

    01001100 01100101 00100000 01100010 
01101001 01101110 01100001 01101001
01110010 01100101 00101100 00100000 
01100011 00100111 01100101 01110011
01110100 00100000 01101001 01101110 
01101000 01110101 01101101 01100001
01101001 01101110 00101110

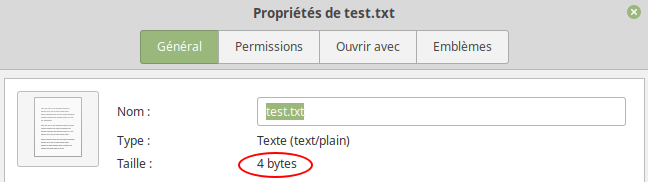
TP2_NSI_2.png

- Quel est la taille du fichier test.txt ?
- Justifier le codage binaire entouré :



Base 16 (Héxadécimale)

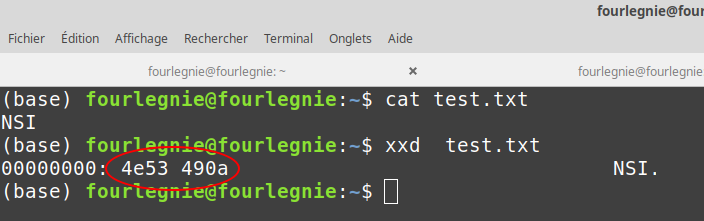
TP2_NSI_4.png

Le terminal affiche le binaire de manière plus condensé cela nous évite de devoir lire de longues enfilades de 0 et de 1

Méthode : Conversion hexadécimale vers décimale

En base 2 (Binaire) , on utilise 2 symboles : 0 et 1
En base 10 (Décimale) on utilise 10 symboles : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
En base 16 (Héxadcimale) on utilise 16 symboles : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

Exemple : (3F7A)16=3 x 163 + 15 x 162 + 7 x 161 + 10 x 160 = 15 x 256 + 7 x 16 + 10 x 1 = 16250

Méthode : Conversion hexadécimale vers décimale

Exemple conversion hexadécimale -> décimale :

4516=4 x 161+5=69

A416=10 x 161+4=164

1- Convertir F5A16 en décimale.
2- Convertir 2019 en héxadécimale.

Compléter le tableau ci-dessous :
Base 16 : héxadécimale Base 10 : décimale Base 2 : binaire
0 0 0000
1 1 0001
2 2 0010
3 3
4 4
5 5
6 6
7 7
8 8
9 9
A 10
B 11
C 12
D 13
E 14
F 15

1- Convertir en décimale puis en binaire.

AB16 =

FF16 =

2- Convertir 111100112 en héxadécimale.

3- Proposer une méthode pour passer plus directement de l'hexadécimale en binaire.

Avec Python

On peut travailler avec des nombres en numération hexadécimale (base 16). Le passage décimal vers hexadécimal se fait avec l’instruction hex : par exemple, hex(60) renvoie la chaîne 0x3c : la notation hexadécimale de 60 est 3C . Inversement, en mettant 0x au début d’un nombre, on indique à Python que le nombre qui suit est en base 16 : l’instruction a=0x4f fait que la variable a prend la valeur 79.
Avec Thonny, taper les instructions suivantes : 
>>> print("Convertir 56 en binaire :",bin(56))

>>> print("Convertir 56 en hexadécimal :",hex(56))
Compléter le tableau ci-dessous :
Base 10 : décimale Base 2 : binaire Base 16 : hexadécimale
12
12
10010110
FADE

TP2_NSI_4.png

Justifier le code hexadécimal entouré.

QUIZZ - TESTEZ VOTRE MAITRISE DE L'HEXADECIMAL

QUIZZ NON FAIT



Python et les chaînes de caractères

Le type string

Une donnée de type string peut se définir comme une suite de caractères. Dans un script python, on peut délimiter une telle suite de caractères, soit par des apostrophes (simple quotes), soit par des guillemets (double quotes). Exemples :
>>> phrase1 = 'les oeufs durs.'
>>> phrase2 = '"Oui", répondit-il,'
>>> phrase3 = "j'aime bien"
>>> print(phrase2, phrase3, phrase1)
"Oui", répondit-il, j'aime bien les oeufs durs.

Les 3 variables phrase1, phrase2, phrase3 sont des variables de type string appelées chaines de caractères.

>>> type(phrase1)
>>> <class 'str'>
>>> type(phrase2)
>>> <class 'str'>
>>> type(phrase3)
>>> <class 'str'>

On peut accédé à un caractère bien déterminé d'une chaîne de caractère :

Tester le code ci-dessous :
>>> chaine="Bonjour"
>>> chaine[0]
>>> chaine[1]
>>> chaine[2]
>>> chaine[3]
>>> len("Bonjour")
Attention : Les données informatiques sont presque toujours numérotées à partir de zéro (et non à partir de un).
C’est le cas pour les caractères d’une chaîne. (Le "B" est le caractère numéro 0)

len()

Déterminer la longueur (c’est-à-dire le nombre de caractères) d’une chaîne, en faisant appel à la fonction intégrée len() :
>>> chaine="Bonjour"
>>> len("Bonjour")
Tester et comprendre les deux codes ci-dessous :
>>> chaine="Bonjour"
>>> for caractere in chaine:
>>>       print(caractere)
>>> chaine="Bonjour"
>>> for i in range(len(chaine)):
>>>       print(chaine[i])

Concéténation

Assembler plusieurs petites chaînes pour en construire de plus grandes. Cette opération s’appelle concaténation. Exemple :
Tester le code ci-dessous :
>>> a = ' Petit poisson '
>>> b = ' deviendra grand '
>>> c = a + b
>>>print(c)

NON FAIT

input()

Cette fonction provoque une interruption dans le programme courant.
L’utilisateur est invité à entrer des caractères au clavier et à terminer avec .
Exemple :
prenom = input("Entrez votre prénom : ")
print("Bonjour," + prenom)
  1. Ecrire un script qui demande à l'utilisateur son prénom et qui affiche :
    Bonjour "prénom", je suis content de te revoir!
  2. Ecrire un script qui demande à l'utilisateur son nom, son prénom et son sexe qui affiche :
    Bonjour "Monsieur ou madame" "nom", votre prénom contient "x" caractères.

Code ...

  1. Écrivez un script qui détermine si une chaîne contient ou non le caractère « e ».
  2. Écrivez un script qui compte le nombre d’occurrences du caractère « e » dans une chaîne.
  3. Écrivez un script qui recopie une chaîne (dans une nouvelle variable), en insérant des astérisques entre les caractères. Ainsi par exemple, « gaston » devra devenir « g*a*s*t*o*n »
  4. Écrivez un script qui recopie une chaîne (dans une nouvelle variable) en l’inversant. Ainsi par exemple, « zorglub » deviendra « bulgroz ».
  5. En partant de l’exercice précédent, écrivez un script qui détermine si une chaîne de caractères donnée est un palindrome (c’est-à-dire une chaîne qui peut se lire indifféremment dans les deux sens), comme par exemple « radar » ou « s.o.s ».

NON FAIT




MICRO PROJET
A l'aide de python, décoder le message suivant :

0100100101101100001000000111100100100000011000010010000000110001
0011000000100000011101000111100101110000011001010111001100100000
0110010001100101001000000111000001100101011100100111001101101111
0110111001101110011001010111001100101100001000000110001101100101
0111010101111000001000000111000101110101011010010010000001100011
0110111101101101011100000111001001100101011011100110111001100101
0110111001110100001000000110110001100101001000000110001001101001
0110111001100001011010010111001001100101001000000110010101110100
0010000001101100011001010111001100100000011000010111010101110100
01110010011001010111001100101110

NON FAIT



Lire l' article

NON LU