Chapitre : Tri insertion V.S tri selection



On complétera au fur et à mesure un fichier Thonny. (insertVSselect.py)

En cas de probleme pour l'obtention des graphique, avec Thonny, vous pouvez utiliser Trinket ( LIEN )

Voici l'algorithme du tri par sélection : 


	
def permuter(L,i,j):
    """
    permute les elements d'indice i et j de L
    exemple :
    >>>permuter([12,7,8,45],1,2)
    [12,8,7,45]
    """
    tmp=L[i]
    L[i]= L[j]
    L[j]=tmp
    return L
	
def tri_select(L):
    n = len(L)
    # la tranche l[0:1] est triée
    for i in range(n - 1):
        for j in range(i+1,n):
            if L[j] < L[i] :
                permuter(L, i, j)
    return L


Tester le tri par selection avec les listes : 


L1=[12,48,5,1,0,9,87]
L2=[k for k in range(15,0,-1)]
L3=[k for  k in range(0,15)]
print("L1=", L1)
print("L2=",L2)
print("L3=",L3)

Ecrire l'affichage obtenu avec Trinket ou Thonny :

L1= [12, 48, 5, 1, 0, 9, 87]
L2= [15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1]
L3= [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]


Ajouter le code ci-desous au début de votre fichier Thonny

import random  #gestion de l'aleatoire
import time # gestion du temps
import matplotlib.pyplot as plt # gestion des graphiques

A l'aide de Thonny, indiquer le rôle de chacune des lignes ci-dessous : 

time1=time.time() 
print('Bonjour')
L=[k for  k in range(5000)]
random.shuffle(L)
tri_select(L)
time2=time.time()
print(time2-time1)

Ecrire vos réponses : 

time1=time.time()           #.....
print('Bonjour')            #.....
L=[k for  k in range(5000)] #.....
random.shuffle(L)           #.....
select_sort(L)              #.....
time2=time.time()           #.....
print(time2-time1)          #.....


  1. Avec le tri par selection, combien de temps faut-il à python pour trier une liste desordonnée (aléatoire) de 10000 valeurs ?
  2. Avec le tri par selection, combien de temps faut-il à python pour trier une liste ordonnée (croissant) de 10000 valeurs ?
  3. Avec le tri par selection, combien de temps faut-il à python pour trier une liste ordonnée ( décroissant) de 10000 valeurs ?
  4. Tester puis expliquer ce que fait la fonction ci-dessous ? 
    5. def temps_tri_selectionV1():
    TEMPS=[] #liste vide
    for i in range(2,300):
        L=[k for  k in range(0,i)]
        random.shuffle(L)        
        time1=time.time() 
        tri_select(L)
        time2=time.time()
        T=time2-time1
        TEMPS.append(T)
    return TEMPS

  1. 10000 valeurs aléatoires : 11.397542715072632 secondes
  2. 10000 valeurs croissanstes : 5.2203757762908936 secondes
  3. 10000 valeurs décroissantes : 22.039355993270874 secondes
  4. Renvoie une liste de temps.
    le 1er tps est celui mis pour trier une liste de 2 valeurs
    le 2ème tps est celui mis pour trier une liste de 3 valeurs
    le 3ème tps est celui mis pour trier une liste de 4 valeurs
    ...
    le dernier tps est celui mis pour trier une liste de 299 valeurs



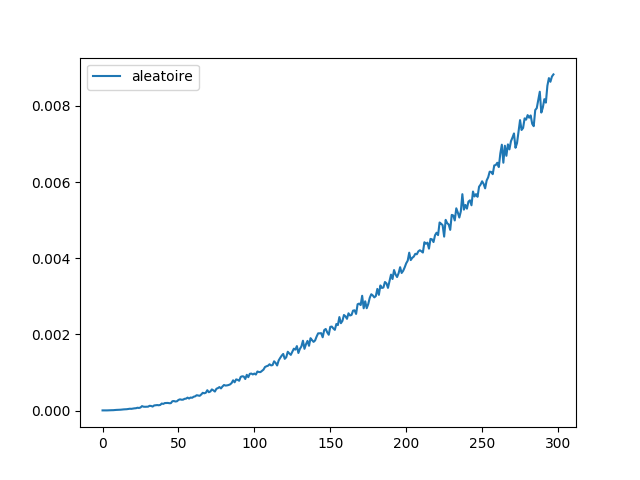
Les 3 lignes ci-dessous permettent de visualiser les temps sous la forme d'un graphique :


plt.plot(temps_tri_selectionV1(), label="aleatoire")
plt.legend()
plt.show()
  1. Tester le code ci-dessus.
  2. Sauvegarder le graphique.
  3. Afficher ci-dessous le graphique obtenu.



  1. Réecrire la fonction temps_tri_selectionV1 ( que l'on nomera temps_tri_selectionV2 ) afin d'obteniur un graphique dans le cas de tri de listes ordonées (décroissante).
  2. Afficher ci-dessous le graphe obtenue.

  1. Réecrire la fonction temps_tri_selectionV1 ( que l'on nomera temps_tri_selectionV3 ) afin d'obteniur un graphique dans le cas de tri de listes ordonées (croissante).
  2. Afficher ci-dessous le graphe obtenu.

  1. Le code ci-dessous permet de mettre plusieurs courbes sur le même graphique.
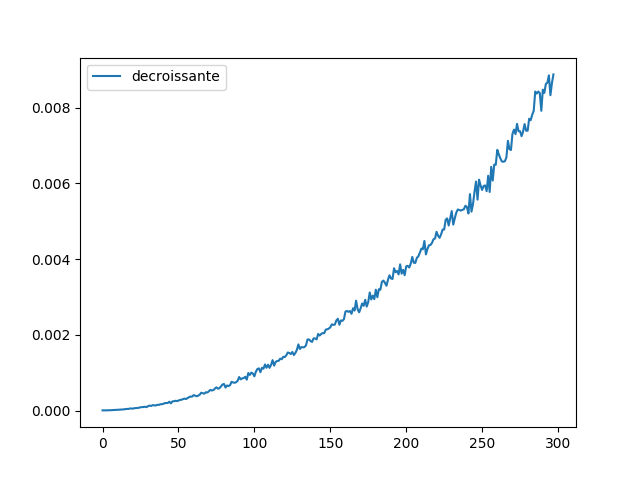
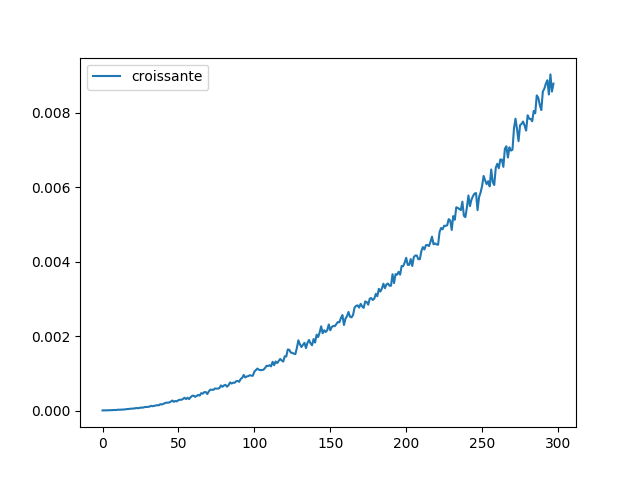
    2. plt.plot(temps_tri_selectionV1(), label="tri select aléa")
plt.plot(temps_tri_selectionV2(), label="tri select décroissant")
plt.plot(temps_tri_selectionV3(), label="tri select croissant")
plt.legend()
plt.show()
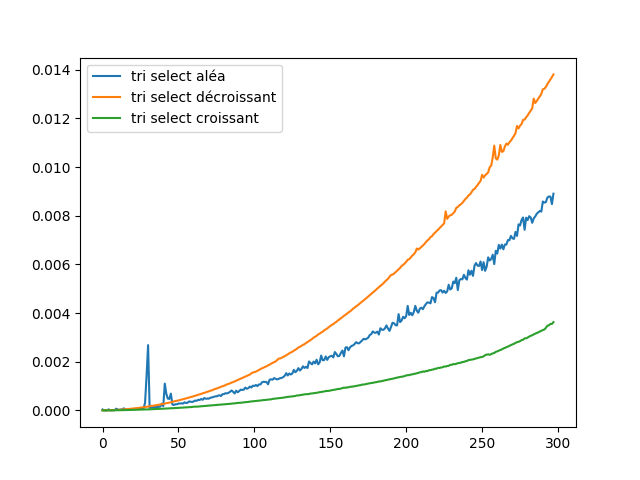
  2. Afficher ci-dessous le graphe obtenu.

COMPARAISON



Le code ci-dessous, vous permet de trier par INSERTION les 3 types de liste (aléatoire, croissant, décroissante)

def tri_insert(L):
    n=len(L)
    for i in range (1,n):
        k=i
        while k>0 and L[k] < L[k-1] :
            permuter(L,k,k-1)
            k=k-1
    return L

Cas aléatoire

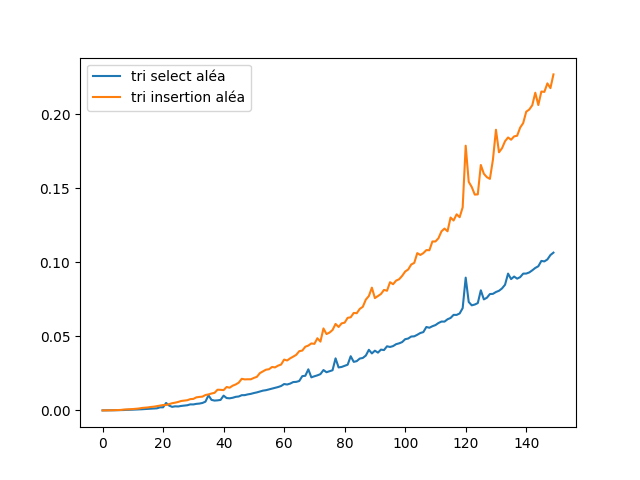
En vous aidant du travail précédent, générer un graphique qui compare le temps mis (par insertion et par selection ) pour trier une liste aléatoire.

On ecrira la fonction : temps_tri_insertV1()



Le pire des cas !

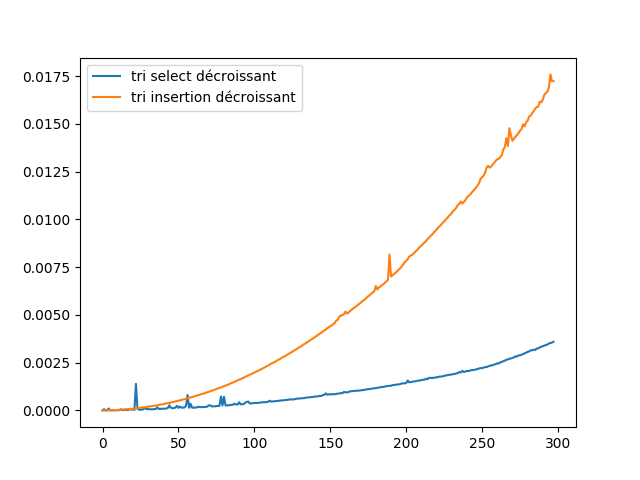
En vous aidant du travail précédent, générer un graphique qui compare le temps mis (par insertion et par selection ) pour trier une liste rangés dans l'odre décroissant.

On ecrira la fonction : temps_tri_insertV2()



Le meilleur des cas !

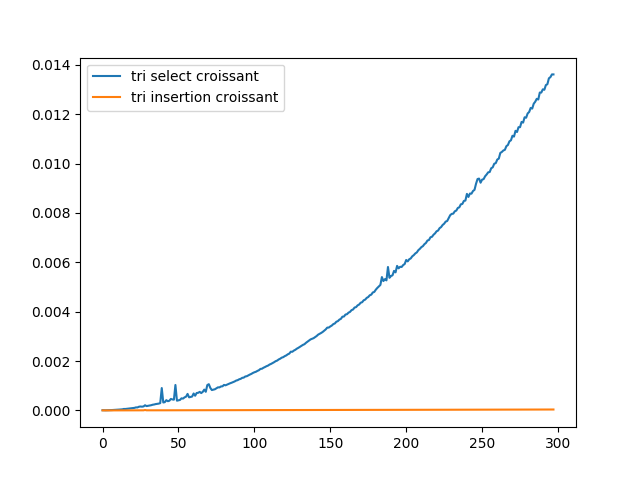
En vous aidant du travail précédent, générer un graphique qui compare le temps mis (par insertion et par selection ) pour trier une liste déja triée.

On ecrira la fonction : temps_tri_insertV3()



Faire une analyse des trois graphiques obtenus.

Quelque soit le type de liste, le tri par selection a une complexité quadratique.
Plus la liste est déja rangée (dans l'ordre croissant) plus le tri insertion aura l'avantage sur le tri par selection.
On le voit très clairement sur le dernier graphique (liste deja triée) où la compléxité est linéaire pour le tri insertion
contre quadratique pour sélection.
Lorque les liste sont aléatoire, les deux tri ont une complexite quadratique mais le tri par sélection est moins couteux en temps.